License is MIT: see https://github.com/JuliaFEM/JuliaFEM.jl/blob/master/LICENSE.md

Natural frequency analysis of 3d frame structure

For general information about Euler-Bernoulli beam theory, see this wikipedia page. The model is a 3d frame, shown in picture.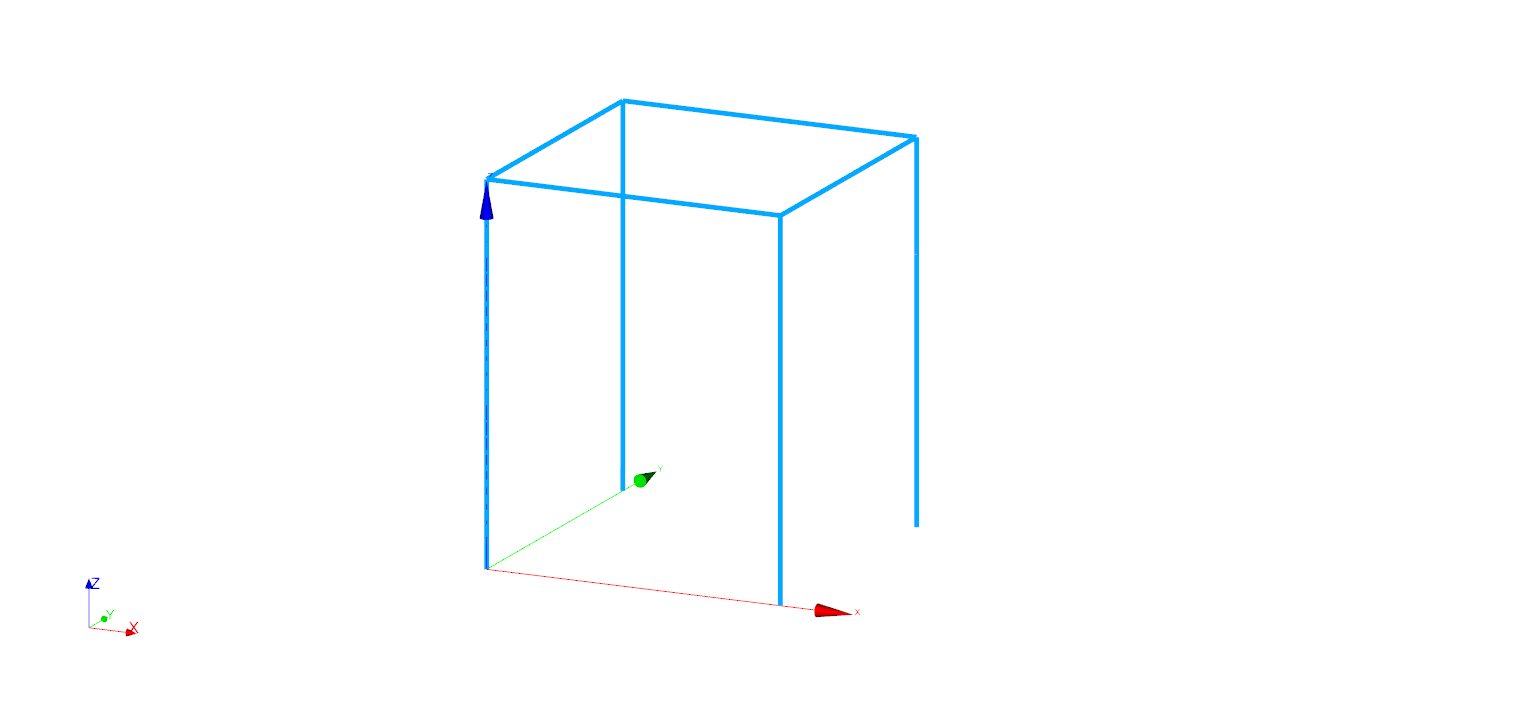

using JuliaFEM, LinearAlgebra

Reading mesh

datadir = Pkg.dir("JuliaFEM", "examples", "3d_frame")
mesh = aster_read_mesh(joinpath(datadir, "model.med"))
println("Number of nodes in a model: ", length(mesh.nodes))

Create beam elements. For 3d model, we need to define at least Young's modulus, shear modulus, density cross-section area, moment of inertia in local coordinate system and polar moment of inertia.

beam_elements = create_elements(mesh, "FRAME")
@info("Number of elements: ", length(beam_elements))
update!(beam_elements, "youngs modulus", 210.0e6)
update!(beam_elements, "shear modulus", 84.0e6)
update!(beam_elements, "density", 7850.0e-3)
update!(beam_elements, "cross-section area", 20.0e-2)
update!(beam_elements, "torsional moment of inertia 1", 10.0e-5)
update!(beam_elements, "torsional moment of inertia 2", 10.0e-5)
update!(beam_elements, "polar moment of inertia", 30.0e-5)

The direction of beam is defined in same way than in ABAQUS. That is, we have a tangent direction and one normal direction. The third direction is then cross product of tangent and normal. Because the second area moment is same in both directions, we can choose normal direction freely.

for element in beam_elements
    X1, X2 = element("geometry", 0.0)
    t = (X2-X1)/norm(X2-X1)
    I = [1.0 0.0 0.0; 0.0 1.0 0.0; 0.0 0.0 1.0]
    k = indmax([norm(cross(t, I[:,k])) for k in 1:3])
    n = cross(t, I[:,k])/norm(cross(t, I[:,k]))
    update!(element, "normal", n)
end

Create boundary conditions: fix all degrees of freedom for nodes in a set FIXED. Here we first create elements of type Poi1 for each node j in set FIXED, update geometry field and then create new fields fixed displacmeent 1, fixed displacement 2, and so on, where the displacement / rotation is prescribed.

bc_elements = [Element(Poi1, [j]) for j in mesh.node_sets[:FIXED]]
update!(bc_elements, "geometry", mesh.nodes)
for i=1:3
    update!(bc_elements, "fixed displacement $i", 0.0)
    update!(bc_elements, "fixed rotation $i", 0.0)
end

Create a problem, containing beam elements and boundary conditions:

frame = Problem(Beam, "3d frame", 6)
add_elements!(frame, beam_elements)
add_elements!(frame, bc_elements)

Perform modal analysis

analysis = Analysis(Modal)
xdmf = Xdmf(joinpath(datadir, "3d_frame_results"); overwrite=true)
add_results_writer!(analysis, xdmf)
add_problems!(analysis, frame)
run!(analysis)
close(xdmf)

Each Analysis can have properties, e.g. time, maximum number of iterations, convergence tolerance and so on. Eigenvalues of calculation are stored as a properties of analysis:

freqs = sqrt.(step.properties.eigvals) / (2*pi)
println("Natural frequencies [Hz]: $(round.(freqs, 2))")

This page was generated using Literate.jl.